L'albero portaelica: le frecce e i giri critici in navigazione

In questa quarta ed ultima parte dell’articolo proseguiamo il calcolo, iniziato nella terza parte, delle sollecitazioni dinamiche per valutare le frecce che si creano nella linea d’asse, mentre la nave è in navigazione, e di conseguenza calcolare il numero dei giri critici, che si potrebbero creare.

La sollecitazione ideale alternata è data da

\(\sigma_{ia} = \sqrt {{\sigma^2}_{fa} + (2 \cdot K_t \cdot \tau_a)^2}\)

dove

\(\sigma_{ia}\) = Sollecitazione alternata determinata dal momento flettente

\(\tau_a\) = Sollecitazione vibrante di torsione = \(0,05 \cdot \tau\)

\(\tau\) = Sollecitazione tangenziale

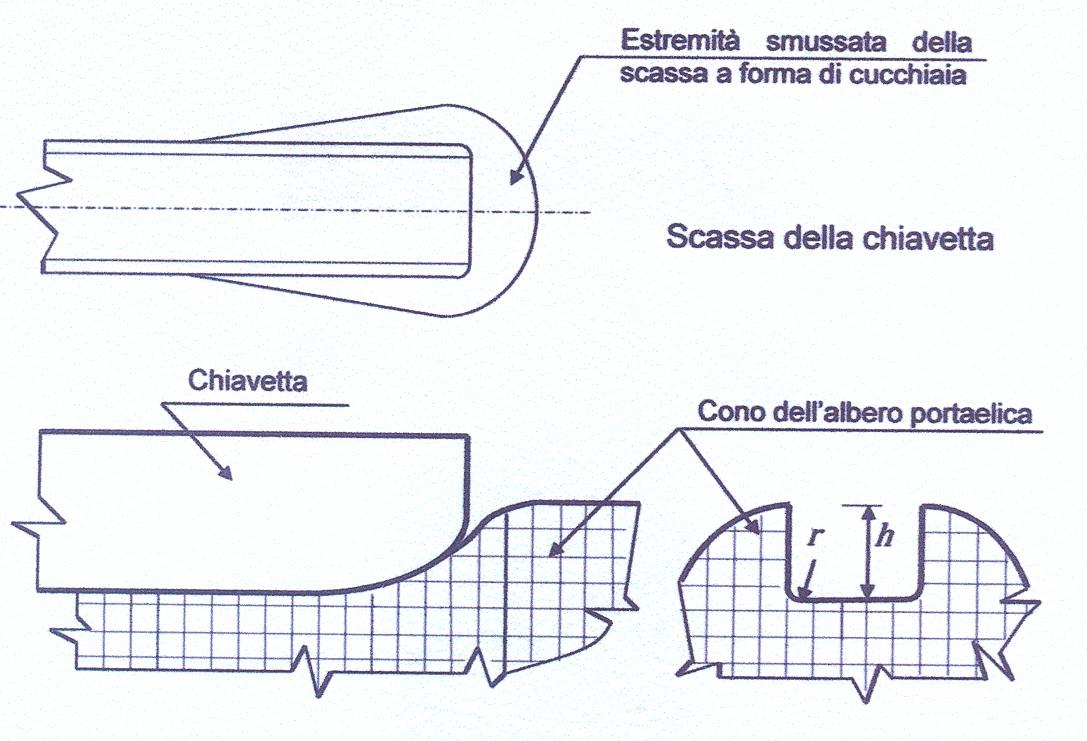
il fattore \(K_t\) negli angoli delle scasse per le chiavette (Figura 8) dipende dal rapporto fra il raggio \(r\) e la profondità \(h\). Il rapporto \(r/h\) non dovrà mai essere inferiore a 0,1 e il valore di \(K_t\) è compreso tra 1,25 e 2,5. La chiavetta è una barretta di acciaio di sezione rettangolare posta metà in una scanalatura o scassa del mozzo dell’elica e metà nella scassa del cono dell’albero portaelica, in modo tale che l’elica è vincolata all’albero e ruota con esso. L’estremità prodiera della scassa della chiavetta deve essere lontana dalla estremità prodiera del mozzo dell’elica e la parte prodiera e poppiera della scassa devono essere arrotondate come la forma di una cucchiaia (Figura 8).

Il numero dei giri critici di un albero portaelica è dato da

\(n_c = {30 \over π} \cdot {\sqrt{({g \over f_i})}}\)

dove

\(g\) = accelerazione di gravità

\(f_i\) = freccia ideale

\(π\) = 3,1415927

Il calcolo della freccia ideale, tra i diversi metodi, si basa sul principio della sovrapposizione degli effetti, che fornisce valori sufficientemente validi.

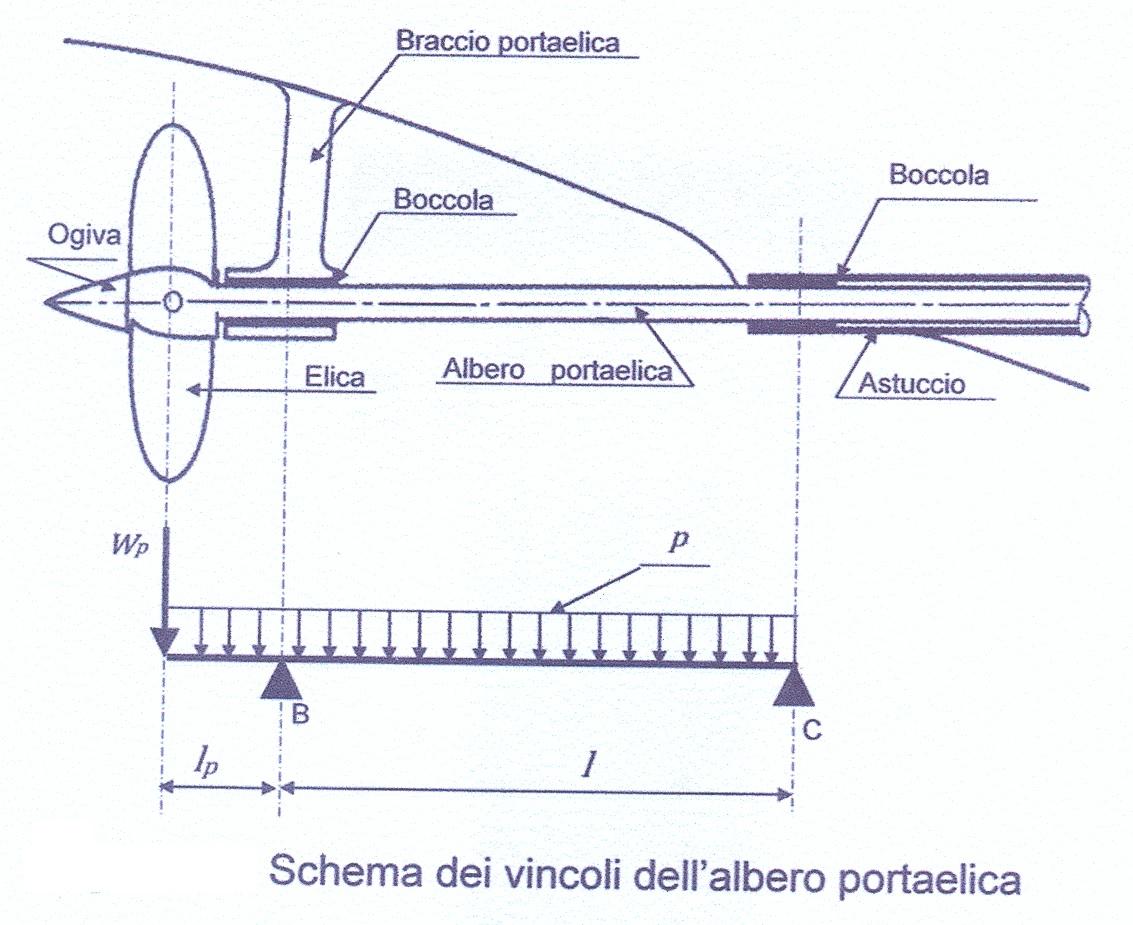
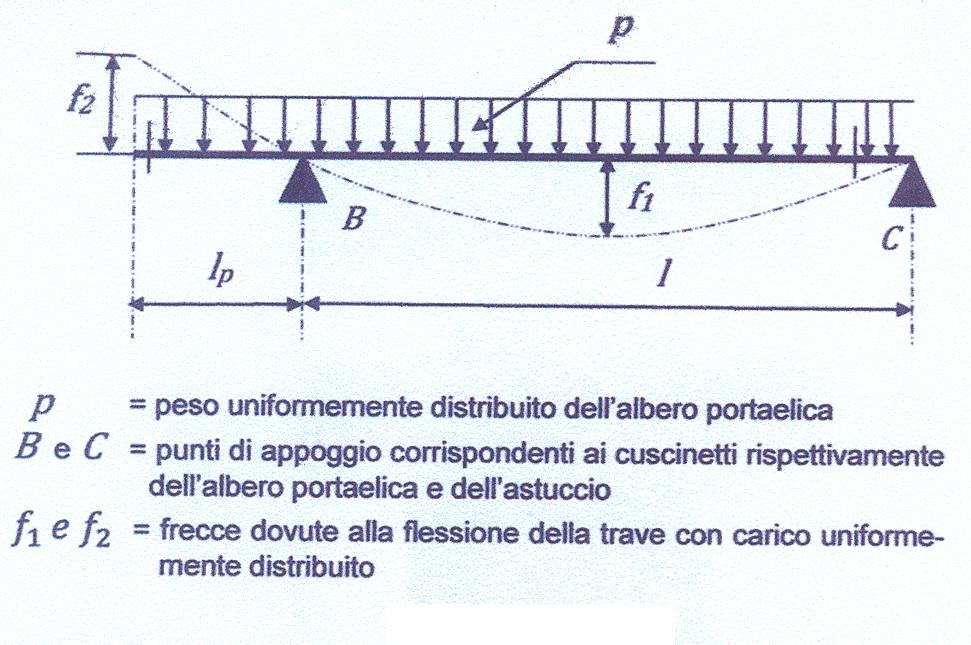
La Figura 5 mostra lo schema della distribuzione dei carichi e dei vincoli. La freccia dell’albero portaelica, con segno positivo (Figura 9), fra gli appoggi, dovuta al carico uniformemente distribuito, è

\(f_1 = {5 \over 384} \cdot {{p \cdot l^4} \over {E \cdot J}}\)

La freccia dell’albero, con segno negativo (Figura 9), all’estremo libero, dovuta al carico uniformemente distribuito, è

\(f_2 = {p \over E \cdot J \cdot 24} \cdot {\{3 \cdot {l_p}^4 + l \cdot l_p \cdot (4 \cdot {l_p}^2 - l^2 ) \}}\)

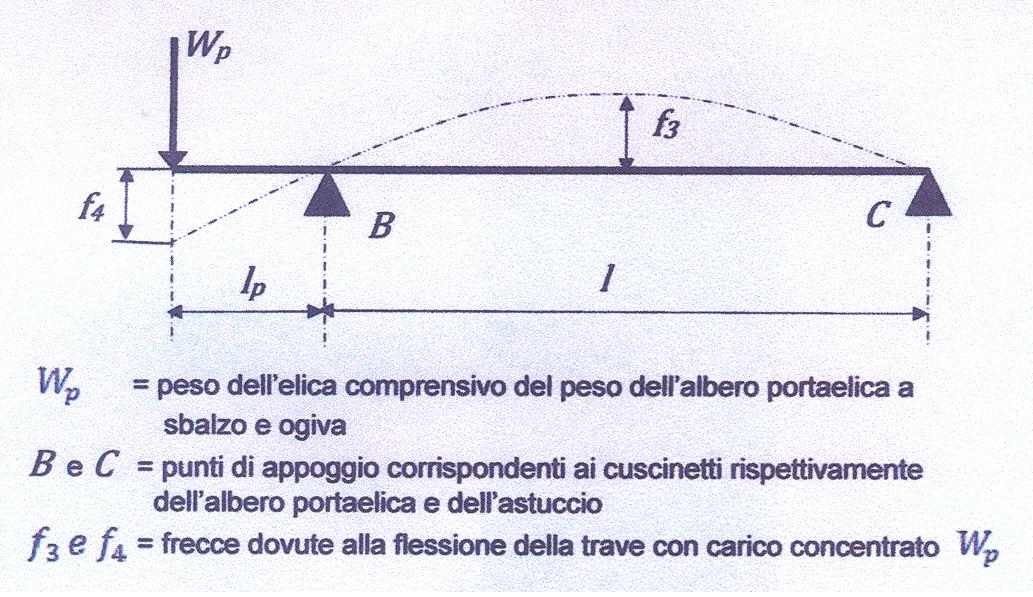
La freccia dell’albero, con segno negativo (Figura 7), nel tratto fra gli appoggi, dovuta al carico concentrato del peso dell’elica, aumentato del 25% circa per tenere conto dell’acqua trascinata, e relativo pezzo di albero a sbalzo, è

\(f_3 = {W_p \cdot l_p \cdot l^2 \over 15,59 \cdot E \cdot J}\)

La freccia dell’albero, con segno positivo (Figura 7), all’estremo libero, dovuta al carico concentrato del peso dell’elica, aumentato del 25% circa per tenere conto dell’acqua trascinata, e relativo pezzo di albero a sbalzo, è

\(f_4 = {W_p \cdot {l_p}^2 \cdot (l_p + l) \over 3 \cdot E \cdot J}\)

La freccia totale dell’albero portaelica fra gli appoggi è

\(f^{'} = f_1 + (-f_3)\)

La freccia totale dell’albero portaelica all’estremo libero è

\(f^{"} = f_4 + (-f_2)\)

La freccia ideale è

\(f_i = {{W_p \cdot (f^{"})^2 + p \cdot l \cdot (f^{'})^2} \over {W_p \cdot f^{"} + p \cdot l \cdot f^{'}}}\)

La velocità angolare critica in \(rad/sec\) sarà

\(ω_c = {\sqrt{({g \over f_i})}}\)

Per cui il numero dei giri critici è dato da

\(n_c={ω_c·{30 \over π}}\)

Il numero dei giri critici \(n_c\) deve essere maggiore del 20% circa rispetto a quello massimo di funzionamento dell’asse. Come già detto nella terza parte di questo articolo, il numero dei giri critici è importante per stabilire la distanza massima fra gli appoggi e conseguentemente il diametro dell’asse. Questi dati sono gli elementi più importanti per la progettazione della linea d’assi.

Angelo Sinisi

©PressMare - riproduzione riservata