La stabilità delle navi: momento d'inerzia e forza

In questa seconda parte dell’articolo per capire meglio il concetto e le condizioni di stabilità dell’equilibrio delle navi, dopo aver parlato nella prima parte del centro di gravità, del centro di carena e del momento statico, cercherò di rendere chiaro il significato del momento d’inerzia e della forza.

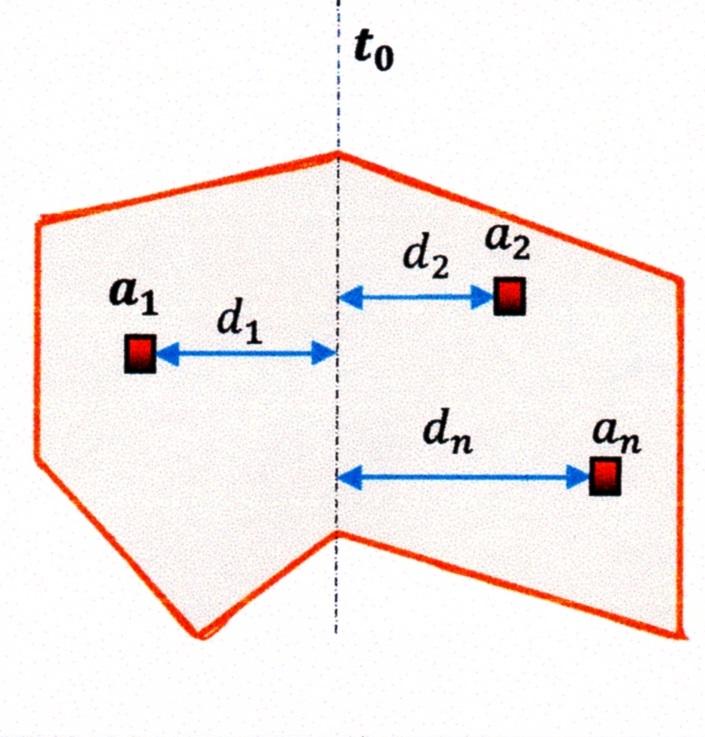
Il “momento d’inerzia assiale” \(J_t\) di una superficie (Figura 7) è la somma dei prodotti delle aree infinitesime \(a_i\) per i quadrati delle distanze \(d_i^2\) dall’asse baricentrico \(t_0\).

Per cui si ha

\(J_t=∑a_i \cdot d_i^2=a_1 \cdot d_1^2+a_2 \cdot d_2^2+a_3 \cdot d_3^2+⋯⋯⋯+a_n \cdot d_n^2\)

Il momento d’inerzia assiale è sempre positivo e la sua unità di misura è quella di una lunghezza alla quarta potenza (\(m^4\)). Il momento d’inerzia può essere concepito come il momento statico di un momento statico, infatti

\(J_t=∑a_i \cdot d_i^2=∑(a_i \cdot d_i ) \cdot d_i=∑(M_i ) \cdot d_i\)

Nella statica della nave il momento d’inerzia della figura di galleggiamento diviso il volume di carena trova il raggio metacentrico trasversale o longitudinale utile per avere l’altezza metacentrica cioè l’indice di stabilità. Infatti

\(r=I_t⁄∇\)

dove

\(r\) = raggio metacentrico trasversale
\(I_t\) = momento d’inerzia trasversale della figura di galleggiamento
\(∇\) = volume di carena

Il secondo principio della dinamica definisce la forza uguale alla massa per l’accelerazione cioè \(F=m \cdot a_c\) dove

\(F\) = forza espressa in N (Newton)
\(m\) = massa definita in Kg (Chilogrammi)
\(a_c\) = accelerazione espressa in \(m⁄s^2 \) (Metri / secondo al quadrato)

Quindi la forza è una grandezza fisica vettoriale che cambia lo stato di quiete o di moto dei corpi. Una forza per essere definita ha bisogno della definizione di un punto di applicazione e di una direzione.

Le condizioni che devono essere soddisfatte affinché una nave liberamente galleggiante sia in equilibrio stabile possono essere dedotte facendo ricorso a concetti comuni e semplici. Se un corpo appoggiato su un piano orizzontale è fermo, noi possiamo dire che esso è in equilibrio. Se vogliamo accertarci che il suo equilibrio sia stabile, tocchiamo il corpo (applichiamo una forza) per deviarlo dalla posizione iniziale. Se, al cessare della nostra azione inclinante, il corpo riprende la sua posizione iniziale, possiamo dire che il corpo è in equilibrio stabile. Nel caso contrario l’equilibrio è instabile.

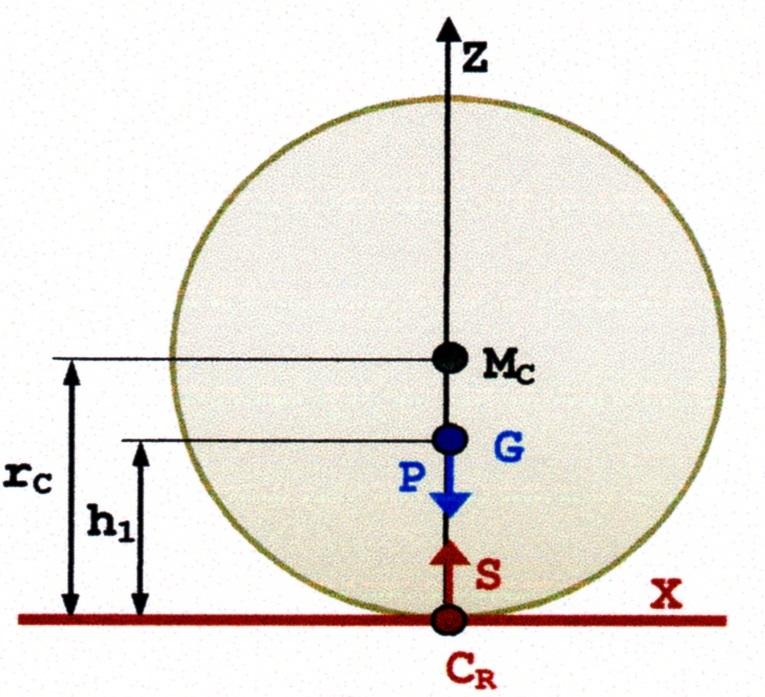
Cercherò di illustrare questo concetto prendendo in considerazione un cilindro (Figura 8) di raggio \(r_c\) e centro \(M_c\) poggiato su un piano orizzontale che ha :

\(G\) = posizione del centro di gravità
\(P\) = peso del cilindro
\(S\) = reazione di appoggio
\(C_R\) = punto di applicazione della reazione di appoggio
\(h_1\) = distanza verticale del centro di gravità \(G\) dal piano orizzontale \(X\)
\(b\) = braccio della coppia \(P\) e \(S\) (Figura 9)

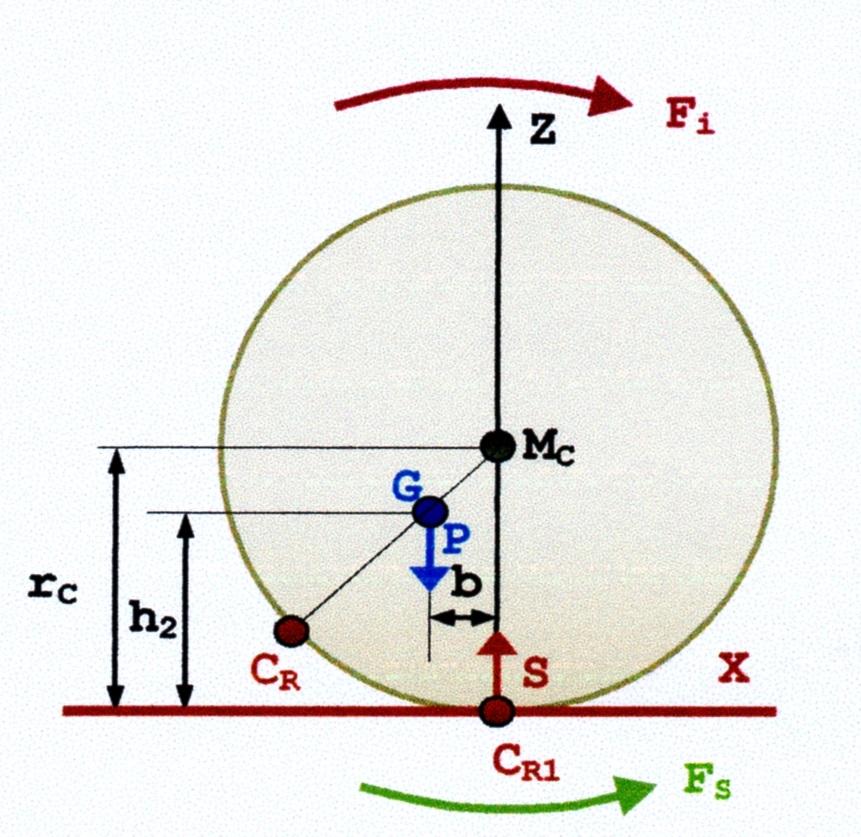
Quando il cilindro è fermo (Figura 8), \(G\) si trova sulla verticale \(Z\) ed il peso \(P\) è uguale alla reazione di appoggio \(S\) applicata nel punto \(C_R\) . Se applichiamo una forza inclinante si otterrà un momento inclinante \(Fi\) secondo la freccia (Figura 9). A tale momento il cilindro contrappone il momento \(Fs\) uguale ed opposto a \(F_i\). Il momento \(F_S\) è generato dalla coppia \(P\) e \(S\) , per cui si ha \(Fs = (P \cdot b)\). E’ evidente che, se cessa il momento \(F_i\) , il cilindro riprende la posizione iniziale della Figura 8.

Infatti, il momento \(F_S\) riporta il cilindro nella sua posizione iniziale e si annulla perché \(b\) si azzera, trovandosi \(P\) e \(S\) sulla stessa verticale \(Z\). Poiché la nuova posizione verticale \(h2\) di \(G\) (Figura 9) dal piano \(X\) è maggiore della precedente \(h1\) (Figura 8) vuol dire che durante l’inclinazione il centro di gravità del cilindro si è sollevato, quindi quando l’equilibrio è stabile il centro di gravità è nella posizione più bassa.

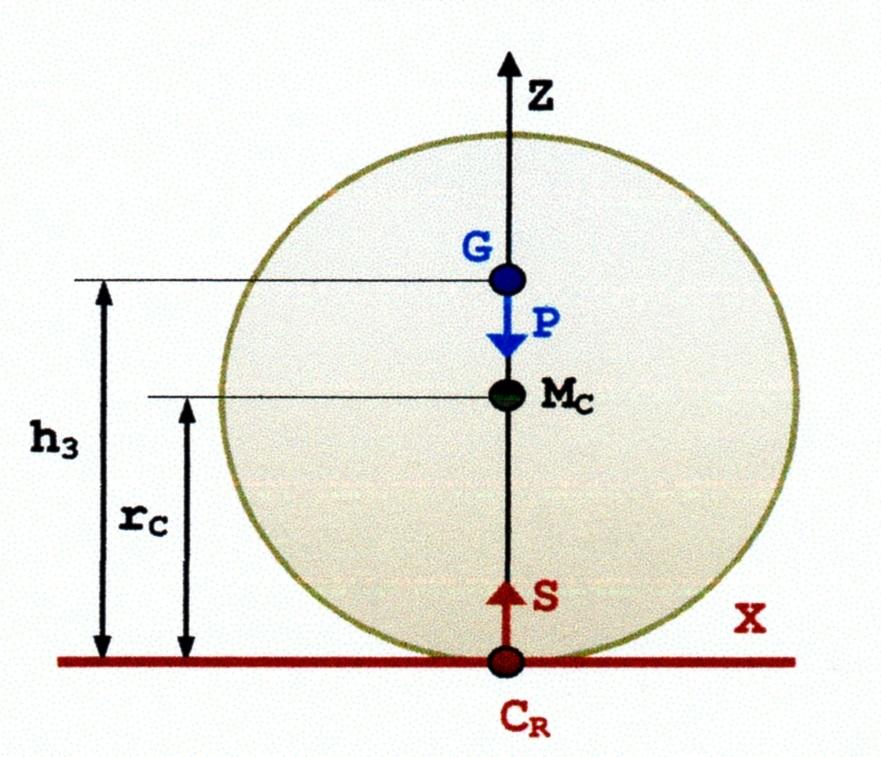
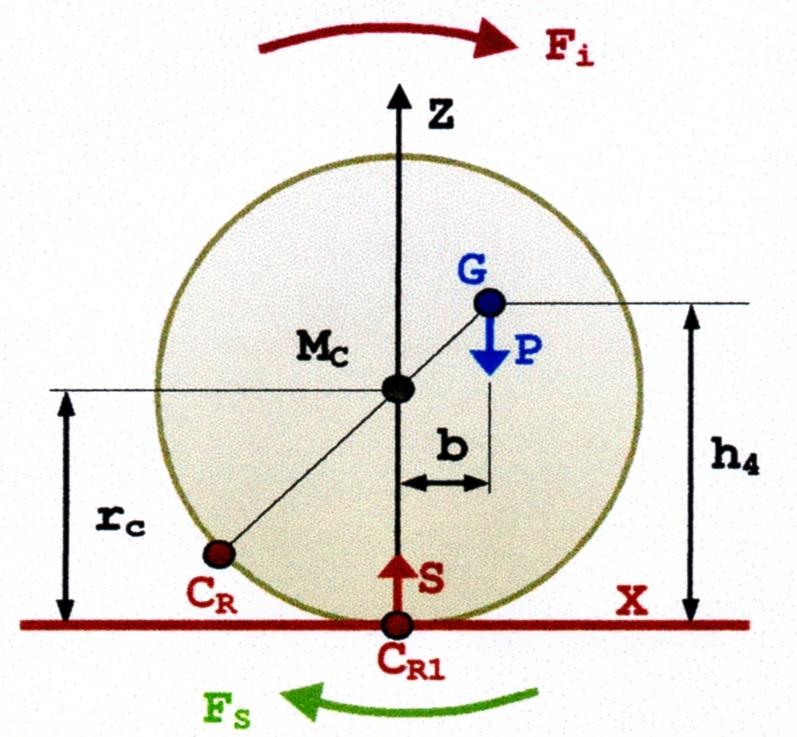
Se vogliamo che l’equilibrio sia stabile, basta che il centro \(Mc\) stia sopra a \(G\), per cui sarà \((r_C-h_1)>0\) come dire \((r – a) > 0\). Supponiamo ora che il cilindro sia disposto come nella Figura 10. E’ evidente che il cilindro è in equilibrio poiché \(P\) e \(S\) sono uguali e \(G\) ed \(M\) stanno sulla stessa verticale \(Z\), ma l’equilibrio è instabile. Infatti, applicando il momento \(F_i\) (Figura 11) il centro di gravità \(G\) si abbassa, la coppia \(P\) e \(S\) genera il momento \(Fs = (P \cdot b)\) , che avendo lo stesso verso del momento \(F_i\) concorre a capovolgere il cilindro.

Quindi l’instabilità dell’equilibrio si può dedurre dalla considerazione che, poiché \(G\) è sopra \(M\), è \((r_C-h_4)<0\) come dire \((r – a) < 0\) .

Dopo quanto detto è facile intuire quale debba essere la condizione affinché la nave sia stabile in una data posizione.

Nella terza parte dell’articolo parlerò della stabilità statica delle navi.

Angelo Sinisi