Lo scafo con carena a geometria variabile - prima parte

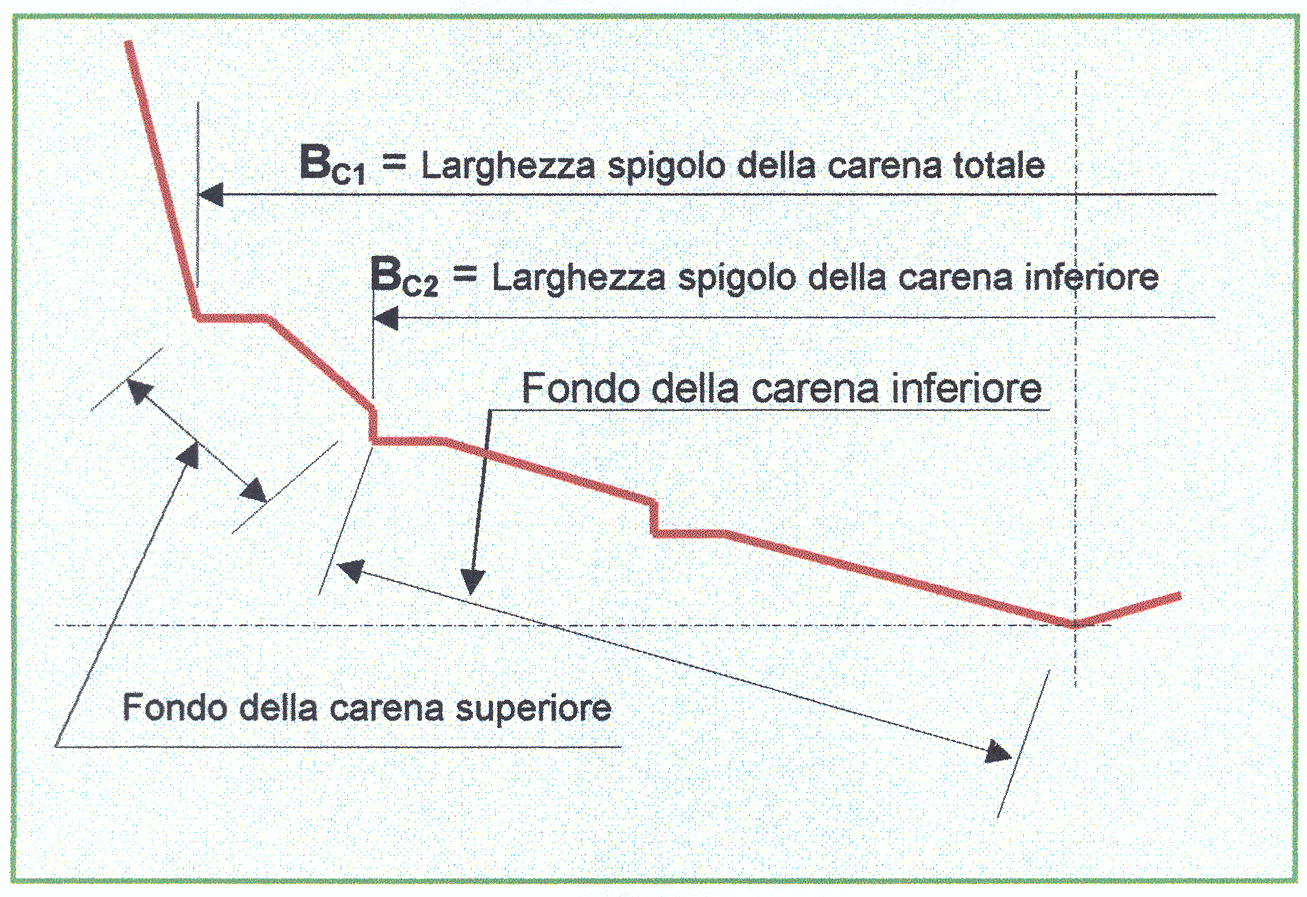
Nei precedenti articoli ho parlato della “Carena Planante”, in questo tratterò di un tipo di Carena Planante denominata “Carena a Geometria Variabile ”.  Con il nome di “Carena a Geometria Variabile”, non si definisce una carena con angolo del fondo variabile da prua a poppa, ma una carena che, a una certa velocità \(V_L\) ,cambia la larghezza del fondo bagnato. Cioè, prima di raggiungere la velocità \(V_L\) ,la larghezza dello spigolo della carena bagnata è \(B_{C1}\)(Figura 1); una volta superata la velocità \(V_L\), la larghezza dello spigolo diventa \(B_{C2}\), più stretta di \(B_{C1}\)(Figura 1).

L’idea di realizzare una carena di questo tipo nacque dalla richiesta di fare una carena che avesse un’alta velocità, una bassa velocità di planata e di conseguenza larga agli spigoli. Larghezza utile per aumentare il volume per l’abitabilità e comodità degli alloggi, molto richiesta dai croceristi. 

I fattori in gioco nel progetto di una carena planante sono: peso, posizione del centro di gravità, velocità, spinta statica e dinamica dell’acqua, angolo d’assetto e resistenza al moto. 

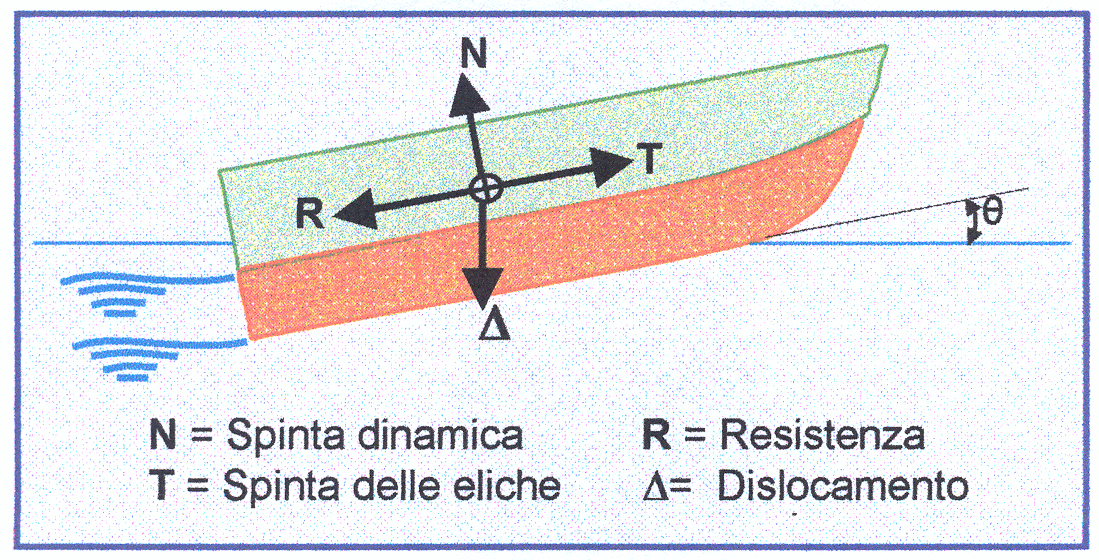
Tutti questi fattori sono molto interdipendenti tra loro per ottenere quell’equilibrio dinamico ottimale relativo a un angolo di assetto tale da dare la minore resistenza possibile (Figura 2). La larghezza, che per gli scafi plananti ha un ruolo di primaria importanza, simile a quello della lunghezza per gli scafi a dislocamento, ha,insieme all’assetto longitudinale e all’angolo di rialzo del fondo, molta influenza sulla resistenza.  Uno scafo a spigolo quando plana si trova in un equilibrio dinamico, determinato dalle forze in gioco. 

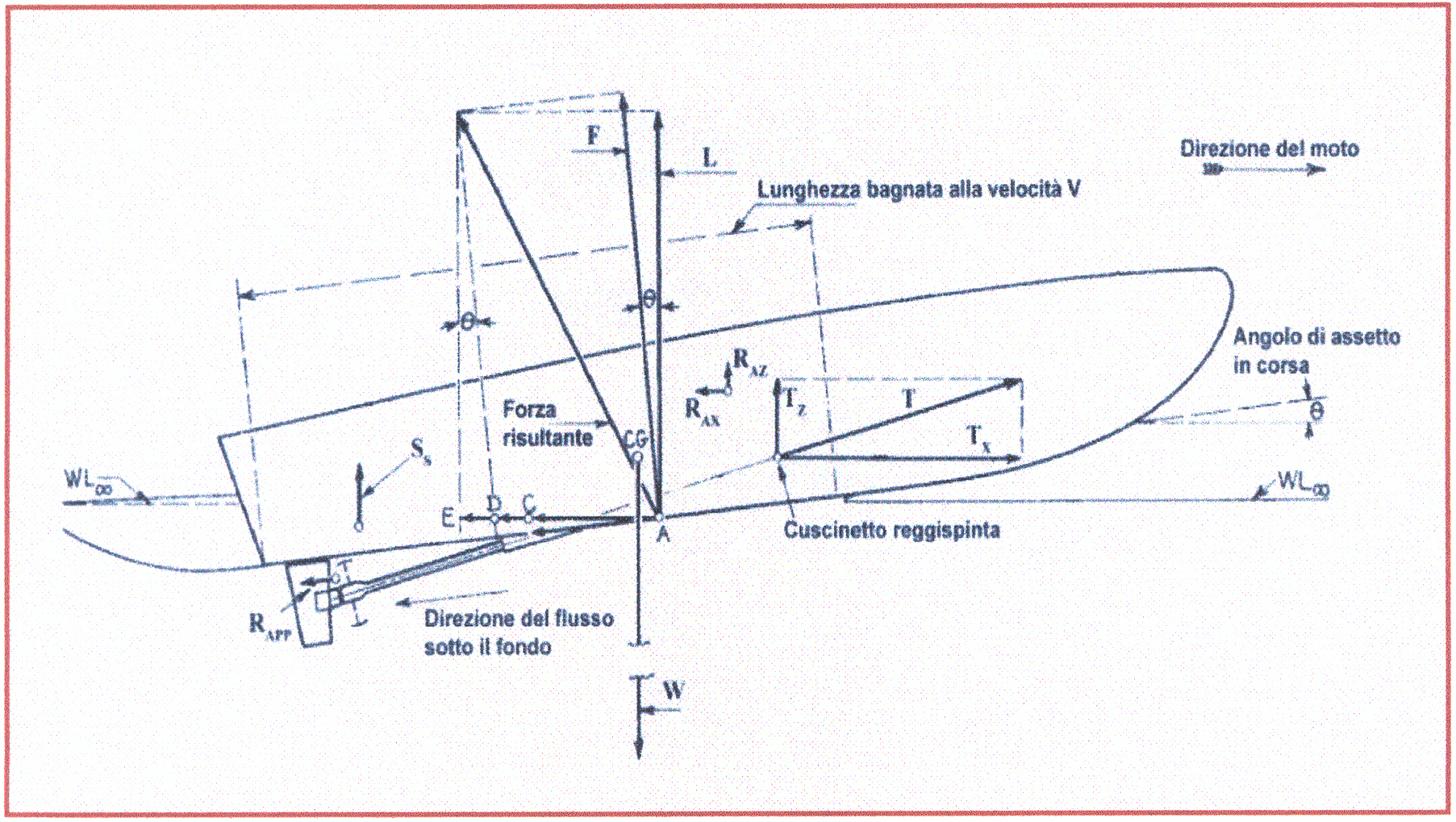
Nella Figura 3 sono schematizzate le principali forze che agiscono sudi uno scafo planante, dove:

Dalle condizioni di equilibrio per le varie forze in gioco, otteniamo, per le sole componenti orizzontali, che la resistenza totale al rimorchio è data da: \(R_T = L \cdot \tan \theta + {({R_F + R_{APP})} \over \cos \theta}+R_{AX}\)

per l’equilibrio verticale si ha: \(W = L + S_S + R_{AZ} + T_Z\)

La resistenza totale al rimorchio di uno scafo planante ha quattro elementi fondamentali, cioè: \(R_T = R_R + R_F + R_{APP} + R_A\)

dove:

l’equazione che calcola la resistenza residua ο d'onda è: \(R_R = \Delta \cdot \tan \theta\)

dove:

Nella seconda parte dell’articolo si parlerà della resistenza d’attrito e della stabilità.

Angelo Sinisi